Awe-Inspiring Examples Of Info About What Does The Y In MX C Mean
Unlocking the Mystery
1. The Starting Point
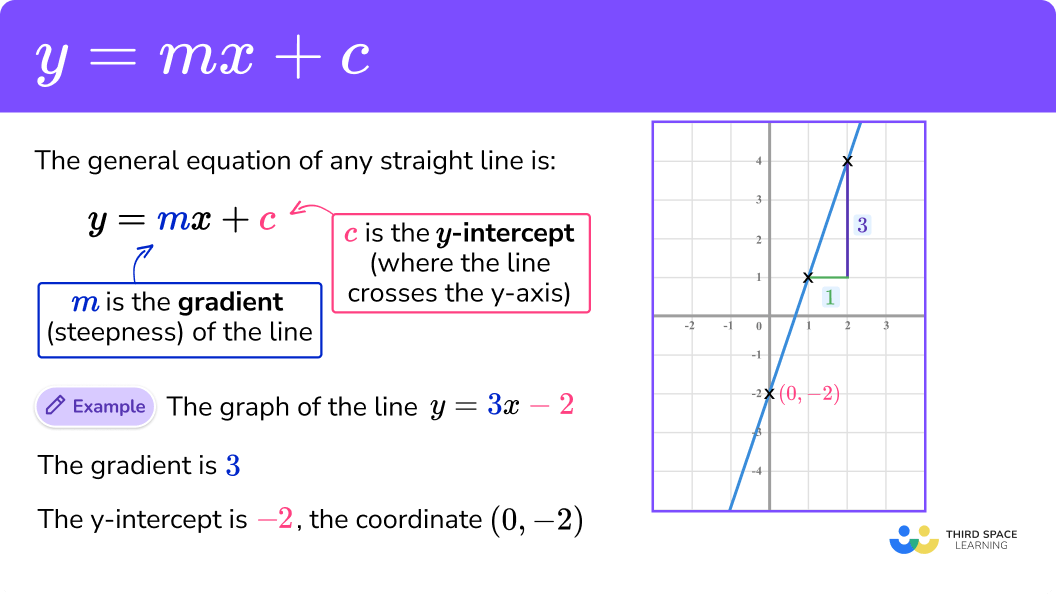
Alright, let's get straight to the point. You've probably seen that equation, "Y = MX + C," lurking in math textbooks or maybe even a dusty corner of your memory. It's the equation of a straight line, and while it might seem intimidating at first glance, it's actually quite friendly once you understand its parts. We're here to break down the enigma of the 'Y', but lets just say, it is as simple as it seems to be.
So, what's the big deal with 'Y'? In this equation, 'Y' represents the dependent variable. Think of it this way: the value of 'Y' depends on what you plug in for 'X'. Its like a reaction — you put something in (X), and you get something out (Y).
To put it another way, 'Y' is the coordinate on the vertical axis (the y-axis) of your graph. When you plot a straight line, you're essentially mapping out all the possible 'Y' values you get for different 'X' values. Imagine 'X' as the input and 'Y' as the output of a machine. Crank the handle (X), and something pops out (Y)!
Don't overthink it! 'Y' is simply the value that the equation spits out once you've done all the calculations on the right side (MX + C). Its the final answer to a mini mathematical puzzle you've just solved.
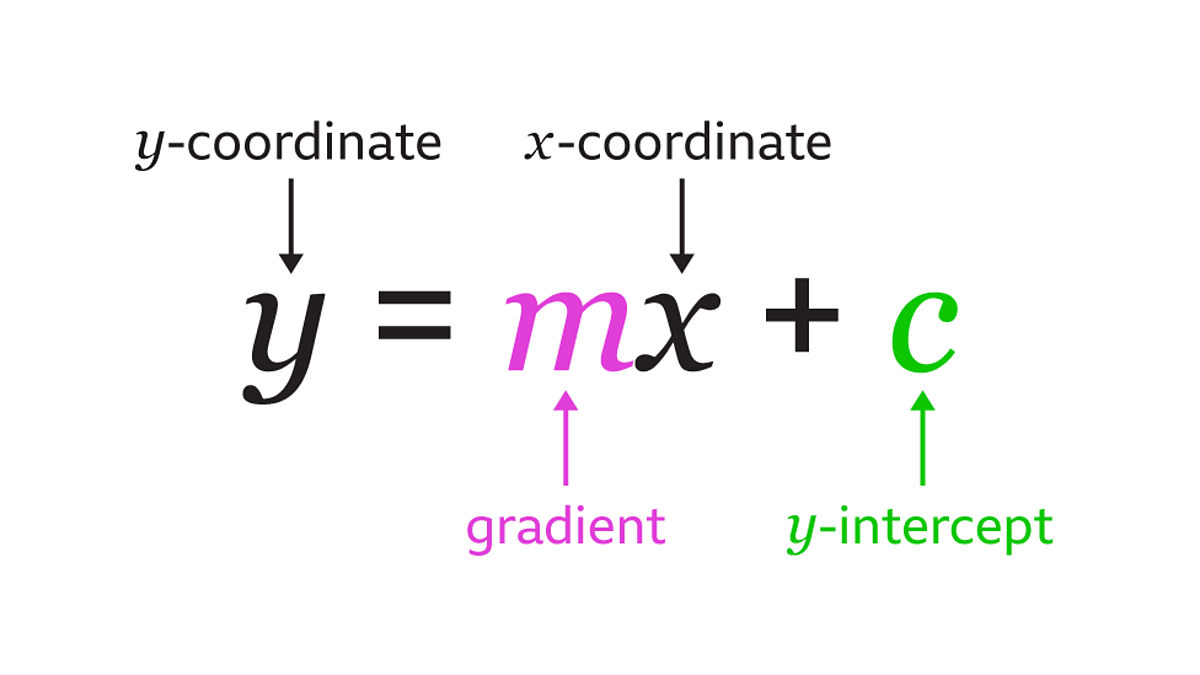
How To Plot A Linear Equation Graph BBC Bitesize
'Y' as the Dependent Variable
2. The Relationship Between 'X' and 'Y'
Okay, so weve established that 'Y' is the dependent variable, but what does that really mean? Let's say we're talking about the cost of renting a car. 'X' could be the number of days you rent the car, and 'Y' would be the total cost. The cost (Y) clearly depends on how long you rent it for (X). Makes sense, right?
Another example: think about the temperature outside. 'X' could be the time of day, and 'Y' could be the temperature at that time. The temperature (Y) is usually dependent on the time of day (X), although there are of course other influences.
The key takeaway here is that 'Y' doesn't just magically appear. Its value is directly influenced by the value of 'X', as well as the 'M' and 'C' values in the equation. It's all interconnected! Each variable needs the other to work.
Understanding this relationship between 'X' and 'Y' is crucial for interpreting graphs and making predictions. If you know the equation of a line, you can plug in any value for 'X' and predict what the corresponding 'Y' value will be. Thats the power of linear equations!
If Y Mx+C Is The Normal At A Point Desiri Beitris
Diving Deeper
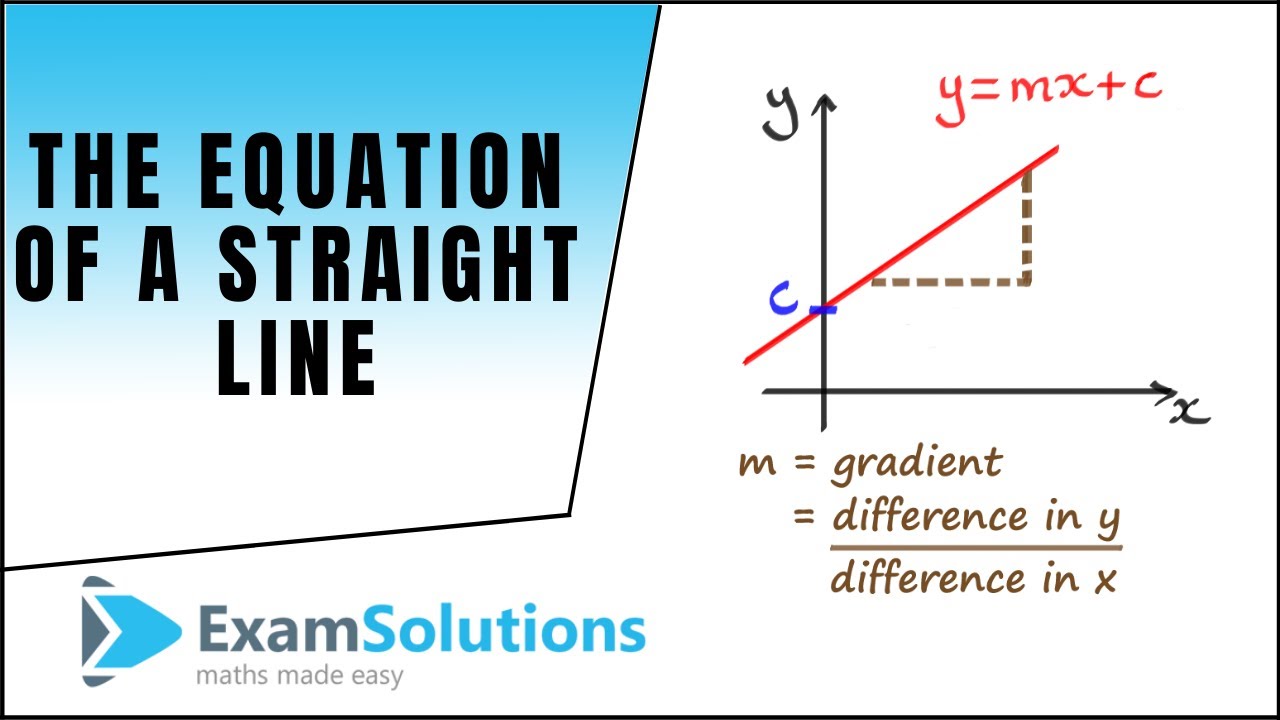
3. 'M' for Slope and 'C' for Intercept
While 'Y' is our star of the show, it's crucial to understand the supporting cast, 'M' and 'C'. 'M' represents the slope of the line, which tells you how steep it is. In our car rental example, 'M' could be the daily rental rate. A higher 'M' means the line is steeper, and the cost increases more quickly for each day you rent the car. Imagine skiing down a hill — the steeper the slope, the faster you go!
'C' is the y-intercept, which is where the line crosses the y-axis. It's the value of 'Y' when 'X' is zero. In the car rental example, 'C' could be a fixed fee or initial charge, no matter how long you rent the car. Its the starting point of the line on the graph.
Together, 'M' and 'C' define the unique characteristics of your straight line. Changing either 'M' or 'C' will change the line's position and direction on the graph. Its like having adjustable controls to fine-tune the line to represent the relationship you want to model.
Thinking back to our temperature example, 'C' might be the temperature at midnight (when the time 'X' is zero), and 'M' might represent the rate at which the temperature increases throughout the day. Understanding 'M' and 'C' helps you paint a complete picture of the relationship between 'X' and 'Y'.
Y Mx C Formula
Practical Applications
4. Real-World Scenarios Using Y = MX + C
Okay, so you know what 'Y' means. Great! But why should you actually care? Well, linear equations are everywhere! They're used in everything from calculating loan payments to predicting sales trends. Understanding them can help you make informed decisions in your daily life.
For instance, let's say you're planning a road trip and want to estimate how much gas you'll need. You could use a linear equation to model the relationship between the distance you drive (X) and the amount of gas you use (Y). By knowing your car's fuel efficiency (related to 'M') and possibly some initial fuel level ('C'), you can make a pretty accurate estimate.
Businesses use linear equations all the time for forecasting. They might track sales data over time and use a linear equation to predict future sales based on past trends. This helps them make decisions about inventory, staffing, and marketing strategies.
Even in science, linear equations are used to model various phenomena. For example, the relationship between the force applied to a spring (X) and the amount it stretches (Y) is often linear (at least within a certain range). So, understanding this simple equation can unlock a world of possibilities!

Putting It All Together
5. Working Through Example Problems
Let's work through an example to solidify your understanding. Suppose you're selling lemonade. Your cost to make each glass of lemonade is $0.50 (this could relate to 'M'). You also have a fixed cost of $10 for supplies like lemons and sugar (this is 'C'). If 'X' is the number of glasses of lemonade you sell, then 'Y' is your total cost: Y = 0.50X + 10.
If you sell 20 glasses of lemonade (X = 20), then your total cost (Y) would be: Y = (0.50 * 20) + 10 = 10 + 10 = $20. So, to make 20 glasses of lemonade, it will cost you $20. If you sell them for $1.50 each, you're making a profit! Well done!
Another example: You are tracking the growth of a plant. Each week (X), the plant grows 2 cm (relates to 'M'). When you started tracking, the plant was already 5 cm tall (this is 'C'). The plant's height (Y) can be represented by the equation: Y = 2X + 5. This simple equation lets you see the height of the plant at any given week.
By practicing with different examples, you'll become more comfortable with identifying the variables and interpreting the results. Remember, the key is to break down the problem into smaller parts and relate each part to the corresponding term in the equation.

FAQ
6. Addressing Common Queries About Y = MX + C
Q: What if 'M' is negative?
A: If 'M' is negative, the line slopes downward. This means that as 'X' increases, 'Y' decreases. Think of it as a decline in something over time, like the temperature decreasing as night approaches.
Q: What happens if 'C' is zero?
A: If 'C' is zero, the line passes through the origin (0,0). This means that when 'X' is zero, 'Y' is also zero. Imagine a scenario where there's no initial cost — you only pay based on usage.
Q: Can 'Y' be negative?
A: Yes, 'Y' can be negative! This simply means that the point is located below the x-axis on the graph. Depending on the context, this could represent a loss, a debt, or a temperature below zero, for instance.
Q: Why is this equation so important?
A: This equation is fundamental because it describes a linear relationship, one of the simplest and most common relationships in the world. It serves as a building block for more complex mathematical models and is essential for understanding many real-world phenomena.